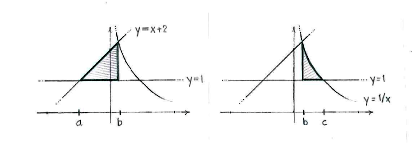Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 2.1:4d

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Zeile 3: Zeile 3:
[[Image:2_1_4_d1.gif|center]]
[[Image:2_1_4_d1.gif|center]]
-
Zeichnen wir alle Kurven im selben Bild, sehen wir dass die Fläche unten von der Geraden <math>y=1</math> begrenzt ist, und oben von den Kurven <math>y=x+2</math> und <math>y=1/x\,</math>.
+
Zeichnen wir alle Kurven im selben Bild, sehen wir, dass die Fläche unten von der Geraden <math>y=1</math> begrenzt ist und oben von den Kurven <math>y=x+2</math> und <math>y=1/x\,</math>.
[[Image:2_1_4_d2.gif|center]]
[[Image:2_1_4_d2.gif|center]]
-
Wir benennen die drei Schnittstellen der Kurven <math>x=a</math>, <math>x=b</math> und <math>x=c</math>, wie in der Figur gezeigt. Wir sehen so dass die Fläche in zwei Teilflächen eingeteilt werden kann. Eine zwischen <math>x=a</math> und <math>x=b</math>, wo die obere Grenze <math>y=x+2</math> ist, und eine zwischen <math>x=b</math> und <math>x=c</math> wo <math>y=1/x</math> die obere Grenze ist.
+
Wir benennen die drei Schnittstellen der Kurven <math>x=a</math>, <math>x=b</math> und <math>x=c</math>, wie in der Figur gezeigt. Wir sehen so, dass die Fläche in zwei Teilflächen eingeteilt werden kann. Eine zwischen <math>x=a</math> und <math>x=b</math>, wo die obere Grenze <math>y=x+2</math> ist und eine zwischen <math>x=b</math> und <math>x=c</math> wo <math>y=1/x</math> die obere Grenze ist.
[[Image:2_1_4_d3.gif|center]]
[[Image:2_1_4_d3.gif|center]]
-
Die Flächen dieser Gebiete ist
+
Die Flächen dieser Gebiete sind
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 28: Zeile 28:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
:Dies ergibt <math>x+2=1</math>, und also <math>x=-1\,</math>. Daher ist <math>a=-1\,</math>.
+
:Dies ergibt <math>x+2=1</math>, also <math>x=-1\,</math>. Daher ist <math>a=-1\,</math>.
Zeile 38: Zeile 38:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
:Eliminieren wir <math>y</math>. erhalten wir eine Gleichung für <math>x</math>,
+
:Eliminieren wir <math>y</math> erhalten wir eine Gleichung für <math>x</math>,
{{Abgesetzte Formel||<math>x+2=\frac{1}{x}\,,</math>}}
{{Abgesetzte Formel||<math>x+2=\frac{1}{x}\,,</math>}}
Zeile 58: Zeile 58:
-
*<math>x=c</math>: Dies ist die Schnittstelle von <math>y=1</math> und <math>y=1/x\,</math>, und also ist <math>x=1\,</math>, und daher <math>c=1\,</math>.
+
*<math>x=c</math>: Dies ist die Schnittstelle von <math>y=1</math> und <math>y=1/x\,</math>, also ist <math>x=1\,</math>, und daher <math>c=1\,</math>.
Zeile 72: Zeile 72:
&= \frac{2-2\sqrt{2}+1}{2} + \sqrt{2} - 1 - \frac{1}{2} + 1\\[5pt]
&= \frac{2-2\sqrt{2}+1}{2} + \sqrt{2} - 1 - \frac{1}{2} + 1\\[5pt]
&= 1 - \sqrt{2} + \frac{1}{2} + \sqrt{2} - 1 - \frac{1}{2} + 1\\[5pt]
&= 1 - \sqrt{2} + \frac{1}{2} + \sqrt{2} - 1 - \frac{1}{2} + 1\\[5pt]
-
&= 1\,,\\[10pt]
+
&= 1\.\\[10pt]
\text{Rechte Fläche}
\text{Rechte Fläche}
&= \int\limits_{\sqrt{2}-1}^1 \Bigl(\frac{1}{x}-1\Bigr)\,dx\\[5pt]
&= \int\limits_{\sqrt{2}-1}^1 \Bigl(\frac{1}{x}-1\Bigr)\,dx\\[5pt]

Version vom 22:39, 21. Aug. 2009

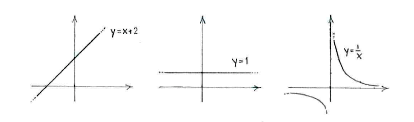
Wir zeichnen die Kurven.

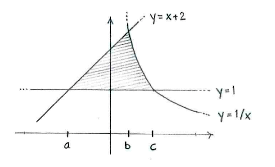
Zeichnen wir alle Kurven im selben Bild, sehen wir, dass die Fläche unten von der Geraden y=1 begrenzt ist und oben von den Kurven y=x+2 und y=1x.

Wir benennen die drei Schnittstellen der Kurven x=a, x=b und x=c, wie in der Figur gezeigt. Wir sehen so, dass die Fläche in zwei Teilflächen eingeteilt werden kann. Eine zwischen x=a und x=b, wo die obere Grenze y=x+2 ist und eine zwischen x=b und x=c wo y=1x die obere Grenze ist.

Die Flächen dieser Gebiete sind

Linke FlächeRechte Fläche=ba(x+2−1)dx=cbx1−1dx

und die gesamte Fläche ist die Summe der beiden Flächen.

Wir suchen also die Schnittstellen:

  • x=a: Die Schnittstelle von y=1 und y=x+2 erfüllt beide Gleichungen:
yy=1=x+2. 
Dies ergibt x+2=1, also x=−1. Daher ist a=−1.


  • x=b: Die Schnittstelle von y=x+2 und y=1x erfüllt beide Gleichungen:
yy=x+2=1x. 
Eliminieren wir y erhalten wir eine Gleichung für x,
x+2=x1
die wir mit x multiplizieren,
x2+2x=1.
Quadratische Ergänzung ergibt:
(x+1)2−12(x+1)2=1=2
Die Wurzeln sind daher x=−12 , und dies ergibt

b=−1+2 . (Die Lösung b=−1−2  liegt links von x=a.)


  • x=c: Dies ist die Schnittstelle von y=1 und y=1x, also ist x=1, und daher c=1.


Die Teilflächen sind also

Unknown control sequence '\.'

und die gesamte Fläche ist

Fläche=(Linke Fläche)+(Rechte Fläche)=1+2−2−ln2−1=2−1−ln2−1.
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:4d“