Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 3.2:1c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Aktuelle Version (15:54, 22. Aug. 2009) (bearbeiten) (rückgängig)
 
Zeile 3: Zeile 3:
{{Abgesetzte Formel||<math>2z+w = 2(2+i)+(2+3i) = 2\cdot 2 + 2 + (2+3)i = 6+5i</math>}}
{{Abgesetzte Formel||<math>2z+w = 2(2+i)+(2+3i) = 2\cdot 2 + 2 + (2+3)i = 6+5i</math>}}
-
Dieseun Punkt können wir in der komplexen Zahlenebene einzeichnen.
+
Diesen Punkt können wir in der komplexen Zahlenebene einzeichnen.
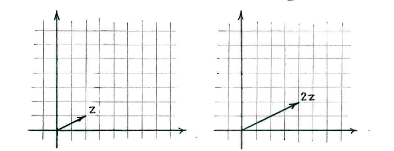
Wenn wir <math>z</math> und <math>w</math> als Vektoren sehen, ist <math>2z</math> doppelt so lang, aber hat dieselbe Richtung wie <math>z</math>.
Wenn wir <math>z</math> und <math>w</math> als Vektoren sehen, ist <math>2z</math> doppelt so lang, aber hat dieselbe Richtung wie <math>z</math>.
Zeile 9: Zeile 9:
[[Image:3_2_1_c1.gif|center]]
[[Image:3_2_1_c1.gif|center]]
-
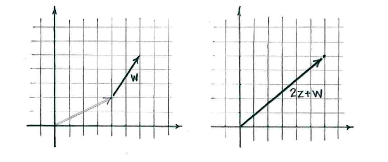
Wir addieren <math>w</math> zu diesen Vektor, und erhalten <math>2z+w</math>.
+
Wir addieren <math>w</math> zu diesen Vektor und erhalten <math>2z+w</math>.
[[Image:3_2_1_c2.gif|center]]
[[Image:3_2_1_c2.gif|center]]

Aktuelle Version

Durch Rechnung erhalten wir

2z+w=2(2+i)+(2+3i)=22+2+(2+3)i=6+5i

Diesen Punkt können wir in der komplexen Zahlenebene einzeichnen.

Wenn wir z und w als Vektoren sehen, ist 2z doppelt so lang, aber hat dieselbe Richtung wie z.

Wir addieren w zu diesen Vektor und erhalten 2z+w.

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:1c“