Lösung 3.3:2a
Aus Online Mathematik Brückenkurs 2
| Zeile 28: | Zeile 28: | ||
und die Wurzeln sind: | und die Wurzeln sind: | ||
| - | {{Abgesetzte Formel||<math>z = 1\cdot\Bigl(\cos\frac{n\pi}{2} + i\sin\frac{n\pi}{2}\Bigr)\,,\quad\text{für }n=0, 1, 2, 3 | + | {{Abgesetzte Formel||<math>z = 1\cdot\Bigl(\cos\frac{n\pi}{2} + i\sin\frac{n\pi}{2}\Bigr)\,,\quad\text{für }n=0, 1, 2, 3</math>}} |
Wir erhalten aber nur vier unterschiedliche Winkel, nämlich <math>0</math>, <math>\pi/2</math>, <math>\pi</math> und <math>3\pi/2</math>, nachdem jeder anderer Winkel sich nur mit einen Multipel von <math>2\pi\,</math> von diesen Winkeln unterscheidet. | Wir erhalten aber nur vier unterschiedliche Winkel, nämlich <math>0</math>, <math>\pi/2</math>, <math>\pi</math> und <math>3\pi/2</math>, nachdem jeder anderer Winkel sich nur mit einen Multipel von <math>2\pi\,</math> von diesen Winkeln unterscheidet. | ||
Version vom 21:09, 22. Aug. 2009
Eine Gleichung der Form "
Wir bringen zuerst
 +isin) =1(cos0+isin0). |
und erhalten die Gleichung
| +isin4)=1(cos0+isin0) |
wo wir den Moivreschen Satz auf der linken Seite benutzt haben. Damit dir rechte und die linke Seite gleich sein sollen, müssen deren Betrag gleich sein und auch deren Argument darf sich nur mit einen Multipel von 
 r44=1=0+2n(n ist eine beliebige natürliche Zahl). |
Also ist
   r=1=2n(n ist eine beliebige natürliche Zahl). |
und die Wurzeln sind:
  cos2n+isin2n für n=0123 |
Wir erhalten aber nur vier unterschiedliche Winkel, nämlich 
22
Die Wurzeln sind daher
 1(cos0+isin0)1(cos(2)+isin(2))1(cos+isin)1(cos(32)+isin(32))=1i−1−i. |
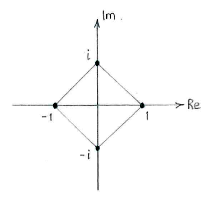
Wir sehen, dass die Lösungen ein Quadrat bilden, wie wir es erwarten, nachdem wir 4 verschiedene Lösungen haben.
