Lösung 1.3:4
Aus Online Mathematik Brückenkurs 2
| Zeile 29: | Zeile 29: | ||
{{Abgesetzte Formel||<math>A''\bigl( 1/\!\sqrt{3}\bigr) = -6\cdot\frac{1}{\sqrt{3}} < 0\,,</math>}} | {{Abgesetzte Formel||<math>A''\bigl( 1/\!\sqrt{3}\bigr) = -6\cdot\frac{1}{\sqrt{3}} < 0\,,</math>}} | ||
| - | also | + | also hat die Flächenfunktion an der Stelle <math>x=1/\!\sqrt{3}</math> ein lokales Maximum. |
Also ist der optimale Punkt <math>P</math> | Also ist der optimale Punkt <math>P</math> | ||
{{Abgesetzte Formel||<math>P = \Bigl(\frac{1}{\sqrt{3}}, 1-\Bigl(\frac{1}{\sqrt{3}} \Bigr)^2\, \Bigr) = \Bigl(\frac{1}{\sqrt{3}}, \frac{2}{3} \Bigr)\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>P = \Bigl(\frac{1}{\sqrt{3}}, 1-\Bigl(\frac{1}{\sqrt{3}} \Bigr)^2\, \Bigr) = \Bigl(\frac{1}{\sqrt{3}}, \frac{2}{3} \Bigr)\,\textrm{.}</math>}} | ||
Version vom 17:57, 9. Sep. 2009
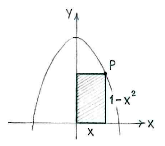
Wir nennen die x-Koordinate des Punktes \displaystyle P \displaystyle x. Die y-Koordinate ist dann \displaystyle 1-x^{2}, da \displaystyle P auf der Kurve \displaystyle y=1-x^{2} liegt.
Die Fläche des Rechtecks ist
| \displaystyle A(x) = \text{(Basis)}\cdot\text{(Höhe)} = x\cdot (1-x^2)\,. |
Wir wollen diese Fläche maximieren.
Wir sehen, dass \displaystyle P im ersten Quadranten liegen muss. Also \displaystyle x\ge 0 und \displaystyle y=1-x^2\ge 0. Wir wissen nun, dass \displaystyle x\le 1 ist. Also suchen wir das Maximum von \displaystyle A(x) im Bereich \displaystyle 0\le x\le 1\,.
Lokale Extremstelle der Fläche sind entweder:
- stationäre Stellen mit \displaystyle f^{\,\prime}(x)=0,
- singuläre Stellen, in denen die Funktion nicht differenzierbar ist, oder
- Randstellen.
Die Funktion \displaystyle A(x) = x(1-x^2) ist überall differenzierbar, also kommt der zweite Fall nicht in Frage. Die Randstellen \displaystyle A(0) = A(1) = 0\, können aber lokale Extremstellen sein (offenbar lokale Minima).
Die Ableitung der Funktion ist
| \displaystyle A'(x) = 1\cdot (1-x^2) + x\cdot (-2x) = 1-3x^2\, |
und wir erhalten die Gleichung \displaystyle x=\pm 1/\!\sqrt{3} für die stationären Stellen.
Nur die Lösung \displaystyle x=1/\!\sqrt{3} erfüllt aber \displaystyle 0\le x\le 1.
Die zweite Ableitung \displaystyle A''(x)=-6x hat in der stationären Stelle den Wert
| \displaystyle A''\bigl( 1/\!\sqrt{3}\bigr) = -6\cdot\frac{1}{\sqrt{3}} < 0\,, |
also hat die Flächenfunktion an der Stelle \displaystyle x=1/\!\sqrt{3} ein lokales Maximum.
Also ist der optimale Punkt \displaystyle P
| \displaystyle P = \Bigl(\frac{1}{\sqrt{3}}, 1-\Bigl(\frac{1}{\sqrt{3}} \Bigr)^2\, \Bigr) = \Bigl(\frac{1}{\sqrt{3}}, \frac{2}{3} \Bigr)\,\textrm{.} |