2.3 Partielle Integration
Aus Online Mathematik Brückenkurs 2
(Added skype and exercise links at the bottom of the page) |
(→Partielle Integration) |
||
| Zeile 25: | Zeile 25: | ||
Partielle Integration kann hilfreich sein, um Produkte zu integrieren. Die Methode stammt von der Ableitungsregel für Produkte. Wenn <math>u</math> und <math>v</math> zwei differenzierbare Funktionen sind, erhalten wir durch die Produktregel die Ableitung | Partielle Integration kann hilfreich sein, um Produkte zu integrieren. Die Methode stammt von der Ableitungsregel für Produkte. Wenn <math>u</math> und <math>v</math> zwei differenzierbare Funktionen sind, erhalten wir durch die Produktregel die Ableitung | ||
| - | {{Abgesetzte Formel||<math>D\,(\,u\, v) = u^{\,\prime} \, v + u \, v | + | {{Abgesetzte Formel||<math>D\,(\,u\, v) = \left( D\, u \right) \, v + u \, D \, v </math>}} |
| + | |||
| + | oder in einer anderen Notation (= Schreibweise) | ||
| + | |||
| + | {{Abgesetzte Formel||<math> \left( \,u \, v \right)^{\, \prime} = u^{\,\prime} \, v + u \, v^{\, \prime} \,\mbox{.}</math>}} | ||
Wenn wir jetzt beide Seiten integrieren, erhalten wir | Wenn wir jetzt beide Seiten integrieren, erhalten wir | ||
| - | {{Abgesetzte Formel||<math>u \, v = \int (\,u^{\,\prime} \, v + u \, v'\,)\,dx = \int u^{\,\prime} \, v\,dx + \int u\, v'\,dx</math>}} | + | {{Abgesetzte Formel||<math>u \, v = \int (\,u v)^{\,\prime} \,dx = \int (\,u^{\,\prime} \, v + u \, v'\,)\,dx = \int u^{\,\prime} \, v\,dx + \int u\, v'\,dx</math>}} |
und so erhalten wir die Regel für partielle Integration. | und so erhalten wir die Regel für partielle Integration. | ||
| Zeile 111: | Zeile 115: | ||
{{Abgesetzte Formel||<math>\int e^x \cos x \, dx = e^x \cos x + e^x \sin x - \int e^x \cos x \, dx</math>}} | {{Abgesetzte Formel||<math>\int e^x \cos x \, dx = e^x \cos x + e^x \sin x - \int e^x \cos x \, dx</math>}} | ||
| - | Sammeln wir alle | + | Sammeln wir alle Integrale auf der linken Seite, so erhalten wir |
{{Abgesetzte Formel||<math>\int e^x \cos x \, dx = {\textstyle\frac{1}{2}}e^x ( \cos x + \sin x) + C\,\mbox{.}</math>}} | {{Abgesetzte Formel||<math>\int e^x \cos x \, dx = {\textstyle\frac{1}{2}}e^x ( \cos x + \sin x) + C\,\mbox{.}</math>}} | ||
Version vom 11:36, 10. Sep. 2009
| Theorie | Übungen |
Inhalt:
- Partielle Integration.
Lernziele:
Nach diesem Abschnitt solltest Du folgendes wissen:
- Wie die partielle Integration hergeleitet wird.
- Wie man Integrale durch partielle Integration, kombiniert mit Substitutionen, löst.
Partielle Integration
Partielle Integration kann hilfreich sein, um Produkte zu integrieren. Die Methode stammt von der Ableitungsregel für Produkte. Wenn
 Du Du v+uDv v+uDv |
oder in einer anderen Notation (= Schreibweise)
 uv uv  =u =u v+uv v+uv . . |
Wenn wir jetzt beide Seiten integrieren, erhalten wir
 (uv) (uv) dx= dx= (u (u v+uv v+uv )dx= )dx= u u vdx+ vdx+ uv uv dx dx |
und so erhalten wir die Regel für partielle Integration.
Partielle Integration:
 uv uv dx=uv− dx=uv− u u vdx. vdx. |
Wenn man Probleme mit partieller Integration löst, erhofft man sich, dass das Integral  u
u vdx
vdx  uv
uv dx
dx 

Obwohl partielle Integration sehr hilfreich sein kann, gibt es keine Garantie, dass es zu einem einfacheren Integral führt. Oft muss man sorgfältig wählen, welche Funktion 
Beispiel 1
Bestimme das Integral  xsinxdx
xsinxdx
Wenn wir  =x
=x =cosx
=cosx 2
2
 xsinxdx=2x2sinx− xsinxdx=2x2sinx− 2x2cosxdx. 2x2cosxdx. |
Dieses Integral ist aber nicht einfacher zu lösen als das ursprüngliche Integral.
Wenn wir aber  =sinx
=sinx =1
=1
 xsinxdx=−xcosx− xsinxdx=−xcosx− −1 −1 cosxdx=−xcosx+sinx+C. cosxdx=−xcosx+sinx+C. |
Beispiel 2
Bestimme das Integral  x2lnxdx
x2lnxdx
Wir wählen  =x2
=x2 =1
=1 x
x 3
3
 x2lnxdx=3x3lnx− x2lnxdx=3x3lnx− 3x3x1dx=3x3lnx−31 3x3x1dx=3x3lnx−31 x2dx=3x3lnx−313x3+C=31x3(lnx−31)+C. x2dx=3x3lnx−313x3+C=31x3(lnx−31)+C. |
Beispiel 3
Bestimme das Integral  x2exdx
x2exdx
Wir wählen  =ex
=ex =2x
=2x
 x2exdx=x2ex− x2exdx=x2ex− 2xexdx. 2xexdx. |
Wir müssen hier noch einmal partielle Integration anwenden, um das Integral  2xexdx
2xexdx  =ex
=ex =2
=2
 2xexdx=2xex− 2xexdx=2xex− 2exdx=2xex−2ex+C. 2exdx=2xex−2ex+C. |
Das ursprüngliche Integral ist
 x2exdx=x2ex−2xex+2ex+C. x2exdx=x2ex−2xex+2ex+C. |
Beispiel 4
Bestimme das Integral  excosxdx
excosxdx
Wir integrieren den Faktor
 excosxdx=excosx− excosxdx=excosx− ex(−sinx)dx=excosx+ ex(−sinx)dx=excosx+ exsinxdx. exsinxdx. |
Dieses Integral berechnen wir durch partielle Integration, indem wir den Faktor
 exsinxdx=exsinx− exsinxdx=exsinx− excosxdx. excosxdx. |
Hier erscheint wieder unser ursprüngliches Integral.
Wir haben also
 excosxdx=excosx+exsinx− excosxdx=excosx+exsinx− excosxdx excosxdx |
Sammeln wir alle Integrale auf der linken Seite, so erhalten wir
 excosxdx=21ex(cosx+sinx)+C. excosxdx=21ex(cosx+sinx)+C. |
Hier erhielten wir kein einfacheres Integral durch partielle Integration, aber wir erhielten eine Gleichung, mit der wir unser Integral lösen konnten. Dies kommt nicht selten vor, wenn man trigonometrische Funktionen und Exponentialfunktionen integriert.
Beispiel 5
Bestimme das Integral  01ex2xdx
01ex2xdx
Das Integral kann als
 01ex2xdx= 01ex2xdx= 012xe−xdx 012xe−xdx |
geschrieben werden. Wählen wir  =e−x
=e−x
 012xe−xdx= 012xe−xdx= −2xe−x −2xe−x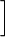 10+ 10+ 012e−xdx= 012e−xdx= −2xe−x −2xe−x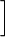 10+ 10+ −2e−x −2e−x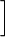 10=(−2e−1)−0+(−2e−1)−(−2)=−e2−e2+2=2−e4. 10=(−2e−1)−0+(−2e−1)−(−2)=−e2−e2+2=2−e4. |
Beispiel 6
Bestimme das Integral  ln
ln x dx
x dx
Zuerst machen wir die Substitution  x
x  2
2 x=dx
x=dx 2u
2u
 ln ln xdx= xdx= lnu lnu 2udu. 2udu. |
Danach wenden wir partielle Integration an. Wir leiten den Faktor
 lnu lnu 2udu=u2lnu− 2udu=u2lnu− u2u1du=u2lnu− u2u1du=u2lnu− udu=u2lnu−2u2+C=xln udu=u2lnu−2u2+C=xln x−x2+C=x x−x2+C=x ln ln x−21 x−21 +C. +C. |
Hinweis: Eine andere Möglichkeit besteht darin, den Integrand als  x=21lnx
x=21lnx
Noch Fragen zu diesem Kapitel? Dann schau nach im Kursforum (Du findest den Link in der Student Lounge) oder frag nach per Skype bei ombTutor 

Keine Fragen mehr? Dann mache weiter mit den Übungen .
