2.2 Integration durch Substitution
Aus Online Mathematik Brückenkurs 2
| Theorie | Übungen |
Inhalt:
- Integration by substitution
Lernziele:
Nach diesem Abschnitt sollst Du folgendes können to:
- Understand the derivation of the formula for substitution .
- Solve simple integration problems that require rewriting and / or substitution in one of the steps.
- Know how the limits of integration are to be changed after a variable substitution.
- Know when substitution is allowed.
Substitution, or change of variable
When you cannot directly determine an indefinite integral by inspection (that is, by simple "differentiation in reverse"), other methods or techniques are needed. One such is substitution (sometimes called change of variable), which can be said to be based on the rule for the differentiation of composite functions — the so-called chain rule.
The chain rule  (u(x))u
(u(x))u (x)
(x)
 f f (u(x))u (u(x))u (x)dx=f(u(x))+C (x)dx=f(u(x))+C |
or,
 f(u(x))u f(u(x))u (x)dx=F(u(x))+C, (x)dx=F(u(x))+C, |
where F is a primitive function of f. We compare this with the formula
 f(u)du=F(u)+C. f(u)du=F(u)+C. |
We can see that we have replaced the term  (x)dx
(x)dx (x)
(x) (x)
(x)
Note 1 The method is based on the assumption that all the conditions for integration are satisfied; that is,
Note 2 Replacing  (x)dx
(x)dx
 x x 0 0 x x u=dxdu=u u=dxdu=u (x), (x), |
which, as  x
x
 u u u u (x) (x) x x du=u du=u (x)dx, (x)dx, |
ie., a small change,  (x)dx
(x)dx
Beispiel 1
Determine the integral 2xex2dx
2xex2dx
If one puts  (x)=2x
(x)=2x (x)dx
(x)dx
 2xex2dx= 2xex2dx= ex2 ex2 2xdx= 2xdx= eudu=eu+C=ex2+C. eudu=eu+C=ex2+C. |
Beispiel 2
Determine the integral  (x3+1)3x2dx
(x3+1)3x2dx
Put  =3x2
=3x2
 (x3+1)3x2dx= (x3+1)3x2dx= 3(x3+1)3 3(x3+1)3 3x2dx= 3x2dx= 3u3du=u412+C=112(x3+1)4+C. 3u3du=u412+C=112(x3+1)4+C. |
Beispiel 3
Determine the integral  tanxdx,
tanxdx, 
 2
2 x
x

 2
2
After rewriting  cosx
cosx
 tanxdx= tanxdx= sinxcosxdx= sinxcosxdx=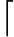  uu uu du=cosx=−sinx=−sinxdx du=cosx=−sinx=−sinxdx  = = −u1du=−ln −u1du=−ln u u +C=−ln +C=−ln cosx cosx +C. +C. |
The limits of integration during variable substitution.
When calculating definite integrals, such as an area, one can go about using variable substitution in two ways. Either one can calculate the integral as usual and then switch back to the original variable and insert the original limits of integration. Alternatively one can change the limits of integration simultaneously with the variable substitution. The two methods are illustrated in the following example.
Beispiel 4
Determine the integral  02ex1+exdx
02ex1+exdx
Method 1
Put  =ex
=ex
 02ex1+exdx= 02ex1+exdx= x=0x=211+udu= x=0x=211+udu= ln ln 1+u 1+u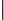 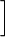 x=2x=0= x=2x=0= ln(1+ex) ln(1+ex)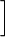 20=ln(1+e2)−ln2=ln21+e2. 20=ln(1+e2)−ln2=ln21+e2. |
Note that the limits of integration must be written in the form
 02ex1+exdx= 02ex1+exdx= 0211+udu etc. 0211+udu etc. |
Method 2
Put  =ex
=ex
 02ex1+exdx= 02ex1+exdx= 1e211+udu= 1e211+udu= ln ln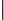 1+u 1+u  1e2=ln(1+e2)−ln2=ln21+e2. 1e2=ln(1+e2)−ln2=ln21+e2. |
Beispiel 5
Determine the integral  0
0
 2sin3xcosxdx
2sin3xcosxdx
The substitution 
 2)=1
2)=1
 0 0 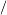 2sin3xcosxdx= 2sin3xcosxdx= 01u3du= 01u3du= 41u4 41u4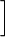 10=41−0=41. 10=41−0=41. |
![[Image]](/wikis/2009/bridgecourse2-TU-Berlin/img_auth.php/metapost/6/9/c/69c86b3fbe07b4e56291d13e076b36bf.png)
| The figure on the left shows the graph of the integrand sin³x cos x and the figure on the right the graph of integrand u³ which is obtained after the variable substitution. The change of variable modifies the integrand and the interval of the integration. The integrals value, the size of the area, is not changed however. |
Beispiel 6
Examine the following calculation
  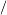 2− 2− 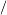 2cosxsin2xdx= 2cosxsin2xdx=    u=sinxdu=cosxdxu(− u=sinxdu=cosxdxu(−  2)=−1u( 2)=−1u(  2)=1 2)=1    = = 1−11u2du= 1−11u2du= −u1 −u1 1−1=−1−1=−2. 1−1=−1−1=−2. |
|
This calculation, however, is wrong, which is due to the fact that A necessary condition in the theory is that |
|

