Lösung 1.3:1c
Aus Online Mathematik Brückenkurs 2
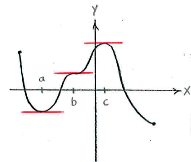
The function has zero derivative at three points, \displaystyle x=a, \displaystyle x=b and \displaystyle x=c (see picture below), which are therefore the critical points of the function.
The point \displaystyle x=b is an inflexion point because the derivative is positive in a neighbourhood both to the left and right.
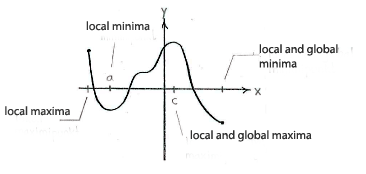
At the left endpoint of the interval of definition and at \displaystyle x=c, the function has local maximum points , because the function takes lower values at all points in the vicinity of these points. At the point \displaystyle x=a and the right endpoint, the function has local minimum points.
Also, we see that \displaystyle x=c is a global maximum (the function takes its largest value there) and the right endpoint is a global minimum.
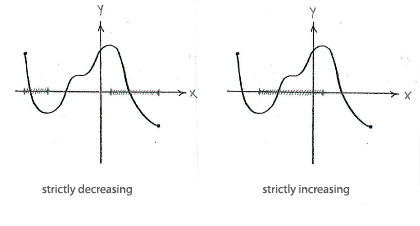
Between the left endpoint and \displaystyle x=a, as well as between \displaystyle x=c and the right endpoint, the function is strictly decreasing (the larger \displaystyle x is, the smaller \displaystyle f(x) becomes), whilst the function is strictly increasing between \displaystyle x=a and \displaystyle x=c (the graph flattens out at \displaystyle x=b, but it isn't constant there).