Lösung 3.3:6
Aus Online Mathematik Brückenkurs 2
We take up the exercise's challenge and solve the equation both in polar form and in the form \displaystyle a+ib.
Polar form
In polar form,
| \displaystyle \begin{align}
z &= r\,(\cos\alpha + i\sin\alpha)\,,\\[5pt] 1+i &= \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,, \end{align} |
and, using de Moivre's formula, the equation becomes
| \displaystyle r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.} |
If both sides are to be equal, their magnitudes must be equal and their arguments must be equal, other than for multiples of \displaystyle 2\pi,
| \displaystyle \left\{\begin{align}
r^2 &= \sqrt{2}\,,\\[5pt] 2\alpha &= \frac{\pi}{4}+2n\pi\,,\quad\text{(n is an arbitrary integer).} \end{align}\right. |
This gives
| \displaystyle \left\{\begin{align}
r &= \sqrt{\sqrt{2}} = \bigl(2^{1/2}\bigr)^{1/2} = 2^{1/4} = \sqrt[4]{2}\,,\\[5pt] \alpha &= \frac{\pi}{8}+n\pi\,,\quad\text{(n is an arbitrary integer),} \end{align}\right. |
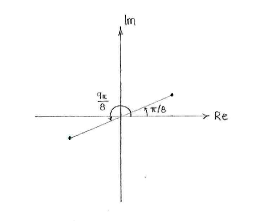
which corresponds two solutions, because all even values of \displaystyle n give the argument \displaystyle \pi/8, to within multiples of \displaystyle 2\pi, and all odd values of \displaystyle n give the argument \displaystyle 9\pi/8, to within a multiple of \displaystyle 2\pi.
Thus, in polar form, we have the solutions,
| \displaystyle z = \left\{\begin{align}
&\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8}\Bigr)\,,\\[5pt] &\sqrt[4]{2}\Bigl(\cos\frac{9\pi}{8} + i\sin\frac{9\pi}{8}\Bigr)\,\textrm{.} \end{align}\right. |
One solution \displaystyle z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8) lies in the first quadrant and the second solution \displaystyle z=\sqrt[4]{2}(\cos (9\pi/8) + i\sin (9\pi/8)) lies in the third quadrant.
Rectangular form
The alternative way to solve the equation is to put \displaystyle z=x+iy and to try to solve the equation for \displaystyle x and \displaystyle y.
If \displaystyle z=x+iy, the equation becomes
| \displaystyle \begin{align}
(x+iy)^2 &= 1+i\,,\\[5pt] x^2-y^2+2xyi &= 1+i\,\textrm{.} \end{align} |
Because both sides' real and imaginary parts must equal each other we have that
| \displaystyle \left\{\begin{align}
x^2 - y^2 &= 1\,,\\[5pt] 2xy &= 1\,\textrm{.} \end{align}\right. |
All the information we need for determining \displaystyle x and \displaystyle y is in these two equations, but it will make things easier if we include an extra relation: the magnitude of both sides should be equal,
| \displaystyle x^2 + y^2 = \sqrt{1^2+1^2} = \sqrt{2}\,\textrm{.} |
Therefore, we have in total three equations,
| \displaystyle \left\{\begin{align}
x^2 -y^2 &= 1\,,\\[5pt] 2xy &= 1\,,\\[5pt] x^2 + y^2 &= \sqrt{2}\,\textrm{.} \end{align}\right. |
If we add the first and the third equations,
| \displaystyle x^2 | \displaystyle {}-{} | \displaystyle y^2 | \displaystyle {}={} | \displaystyle 1 | |
| \displaystyle +\ \ | \displaystyle x^2 | \displaystyle {}+{} | \displaystyle y^2 | \displaystyle {}={} | \displaystyle \sqrt{2} |
| \displaystyle 2x^2 | \displaystyle {}={} | \displaystyle \sqrt{2}+1 | |||
we get that \displaystyle x must be equal to
| \displaystyle x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.} |
If we subtract the first equation from the third equation,
| \displaystyle x^2 | \displaystyle {}+{} | \displaystyle y^2 | \displaystyle {}={} | \displaystyle \sqrt{2} | |
| \displaystyle -\ \ | \displaystyle \bigl(x^2 | \displaystyle {}-{} | \displaystyle y^2 | \displaystyle {}={} | \displaystyle 1\bigr) |
| \displaystyle 2y^2 | \displaystyle {}={} | \displaystyle \sqrt{2}-1 | |||
we obtain that \displaystyle y must be equal to
| \displaystyle y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} |
All in all, this gives us four possible solutions
| \displaystyle \left\{\begin{align}
x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align} \right. |
although we have only taken account of the first and third equations.
The second equation says that the product \displaystyle xy should be positive and then we can directly get rid of solutions in which \displaystyle x and \displaystyle y have different signs. Thus, all that is left is
| \displaystyle \left\{\begin{align}
x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \qquad\text{and}\qquad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. |
Now, we know already that the equation has two solutions, so we can draw the conclusion that these are
| \displaystyle z = \left\{\begin{align}
\sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}\,,\\[5pt] -\sqrt{\frac{\sqrt{2}+1}{2}} - i\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} \end{align}\right. |
If we compare the solution in the first quadrant when it is expressed in polar and rectangular forms, we have
| \displaystyle \sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8} \Bigr) = \sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}} |
and therefore we must have that
| \displaystyle \begin{align}
\cos\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}+1}{2}}\,,\\[5pt] \sin\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} \end{align} |
Thus, we have
| \displaystyle \tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.} |
We can simplify the expression under the square root sign by multiplying top and bottom by the conjugate of the denominator,
| \displaystyle \begin{align}
\tan\frac{\pi}{8} &= \sqrt{\frac{(\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}} = \sqrt{\frac{(\sqrt{2}-1)^2}{(\sqrt{2})^2-1^2}}\\[5pt] &= \sqrt{\frac{(\sqrt{2}-1)^2}{2-1}} = \sqrt{(\sqrt{2}-1)^2} = \sqrt{2}-1\,\textrm{.} \end{align} |