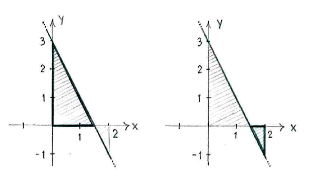Lösung 2.1:1c
Aus Online Mathematik Brückenkurs 2
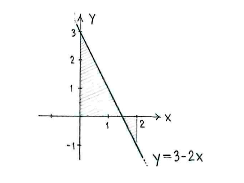
The straight line \displaystyle y=3-2x cuts the x-axis at the point
| \displaystyle y=3-2x=0\quad \Leftrightarrow \quad x=3/2 |
so the part of the line to the right of \displaystyle x=3/2 lies under the y-axis.
When the curve of a function lies both above and below the x-axis, the value of the integral can be interpreted as “an area having a sign”, which means that, for that part where the curve is under the x-axis, we instead subtract the area between the curve and the x-axis.
If we divide up the area between the straight line and the x-axis at \displaystyle x=3/2, we see that the value of the integral is the area of the triangle to the left in the figure below, minus the area of the triangle to the right.
We obtain
| \displaystyle \int\limits_{0}^{2} (3-2x)\,dx = \frac{1}{2}\cdot\frac{3}{2}\cdot 3 - \frac{1}{2}\cdot\frac{1}{2}\cdot 1 = \frac{9}{4} - \frac{1}{4} = 2\,\textrm{.} |