Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 2.1:4c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
First, we need a picture of what the region looks like.
First, we need a picture of what the region looks like.
-
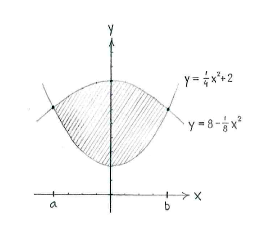
Both curves,
+
Both curves, <math>y=x^2/4+2</math> and <math>y=8-x^2/8</math>, are parabolas, the first with a minimum value <math>y=2</math> when <math>x=0</math>, and the second with a maximum value of <math>y=8</math> when <math>x=0</math>. Roughly speaking, the curves have the appearance shown in the figure below, where the shaded region whose area we are trying to find lies between the curves.
-
<math>y=\frac{1}{4}x^{2}+2</math>
+
-
and
+
-
<math>y=8-\frac{1}{8}x^{2}</math>, are parabolas, the first with a minimum value
+
-
<math>y=\text{2}</math>
+
-
when
+
-
<math>x=0</math>, and the second with a maximum value of
+
-
<math>y=\text{8}</math>
+
-
when
+
-
<math>x=0</math>. Roughly speaking, the curves have the appearance shown in the figure below, where the shaded region whose area we are trying to find lies between the curves.
+
-
 
+
[[Image:2_1_4_c.gif|center]]
[[Image:2_1_4_c.gif|center]]
 +
The region is bounded above by the parabola <math>y=8-x^2/8</math> and below by the parabola <math>y=x^2/4+2</math>. If we can determine the ''x''-coordinates, <math>x=a</math> and <math>x=b</math>, for the points of intersection between the curves, the area we are looking for will be given by
-
The region is bounded above by the parabola
+
{{Displayed math||<math>\text{Area} = \int\limits_{a}^{b} \bigl(\bigl(8-\tfrac{1}{8}x^2\bigr) - \bigl(\tfrac{1}{4}x^2+2\bigr)\bigr)\,dx\,\textrm{.}</math>}}
-
<math>y=8-\frac{1}{8}x^{2}</math>
+
-
and below by the parabola
+
-
<math>y=\frac{1}{4}x^{2}+2</math>. If we can determine the
+
-
<math>x</math>
+
-
-coordinates,
+
-
<math>x=a\text{ }</math>
+
-
and
+
-
<math>x=b</math>, for the points of intersection between the curves, the area we are looking for will be given by
+
-
Area =
+
The integrand is the ''y''-value for the upper parabola minus the corresponding ''y''-value for the lower parabola.
-
<math>\int\limits_{a}^{b}{\left( \left( 8-\frac{1}{8}x^{2} \right)-\left( \frac{1}{4}x^{2}+2 \right) \right)}\,dx</math>
+
 +
At the points where the curves intersect each other, the ''x''- and ''y''-coordinates are equal, which gives the equation system,
-
The integrand is the
+
{{Displayed math||<math>\left\{\begin{align}
-
<math>y</math>
+
y &= 8-\tfrac{1}{8}x^2\,,\\[5pt]
-
-value for the upper parabola minus the corresponding
+
y &= \tfrac{1}{4}x^2+2\,\textrm{.}
-
<math>y</math>
+
\end{align}\right.</math>}}
-
-value for the lower parabola.
+
-
At the points where the curves intersect each other, the
+
If we eliminate ''y'' from this system, we get the following equation for ''x'',
-
<math>x</math>
+
-
- and
+
-
<math>y</math>
+
-
-coordinates are equal, which gives the equation system,
+
-
 
+
{{Displayed math||<math>8-\tfrac{1}{8}x^2 = \tfrac{1}{4}x^2+2\,\textrm{.}</math>}}
-
<math>\left\{ \begin{matrix}
+
-
y=8-\frac{1}{8}x^{2} \\
+
-
y=\frac{1}{4}x^{2}+2 \\
+
-
\end{matrix} \right.</math>
+
-
 
+
-
 
+
-
If we eliminate
+
-
<math>y</math>
+
-
from this system, we get the following equation for
+
-
<math>x</math>,
+
-
 
+
-
 
+
-
<math>8-\frac{1}{8}x^{2}=\frac{1}{4}x^{2}+2</math>
+
 +
If we move the <math>x^2</math>-terms onto one side and the constants onto the other, we obtain
-
If we move the
+
{{Displayed math||<math>\tfrac{1}{4}x^2 + \tfrac{1}{8}x^2 = 8-2\,,</math>}}
-
<math>x^{2}</math>
+
-
terms onto one side and the constants onto the other, we obtain
+
-
 
+
-
 
+
-
<math>\frac{1}{4}x^{2}+\frac{1}{8}x^{2}=8-2</math>,
+
i.e.
i.e.
 +
{{Displayed math||<math>\begin{align}
 +
\bigl(\tfrac{1}{4}+\tfrac{1}{8}\bigr)x^2 &= 6\,,\\[5pt]
 +
\tfrac{3}{8}x^2 &= 6\,,\\[5pt]
 +
x^2 &= 16\,\textrm{.}
 +
\end{align}</math>}}
-
<math>\begin{align}
+
The ''x''-coordinates of the points of intersection are therefore equal to <math>x=-4</math> and <math>x=4\,</math>.
-
& \left( \frac{1}{4}+\frac{1}{8} \right)x^{2}=6 \\
+
-
& \frac{3}{8}x^{2}=6 \\
+
-
& x^{2}=16 \\
+
-
\end{align}</math>
+
-
 
+
-
 
+
-
The
+
-
<math>x</math>
+
-
-coordinates of the points of intersection are therefore equal to
+
-
<math>x=-\text{4 }</math>
+
-
and
+
-
<math>x=\text{4}</math>.
+
The area of the area between the curves is given by
The area of the area between the curves is given by
-
 
+
{{Displayed math||<math>\begin{align}
-
<math>\begin{align}
+
\text{Area} &= \int\limits_{-4}^{4} \Bigl(\Bigl(8-\frac{1}{8}x^2\Bigr)-\Bigl( \frac{1}{4}x^2+2\Bigr) \Bigr)\,dx\\[5pt]
-
& \text{Area}=\int\limits_{-4}^{4}{\left( \left( 8-\frac{1}{8}x^{2} \right)-\left( \frac{1}{4}x^{2}+2 \right) \right)}\,dx \\
+
&= \int\limits_{-4}^{4}\Bigl(8-\frac{1}{8}x^2-\frac{1}{4}x^2-2\Bigr)\,dx\\[5pt]
-
& =\int\limits_{-4}^{4}{\left( 8-\frac{1}{8}x^{2}-\frac{1}{4}x^{2}-2 \right)}\,dx \\
+
&= \int\limits_{-4}^{4}\Bigl(6-\Bigl(\frac{1}{8}+\frac{1}{4}\Bigr)x^2\Bigr)\,dx\\[5pt]
-
& =\int\limits_{-4}^{4}{\left( 6-\left( \frac{1}{8}+\frac{1}{4} \right)x^{2} \right)}\,dx \\
+
&= \int\limits_{-4}^{4}\Bigl(6-\frac{3}{8}x^2\Bigr)\,dx\\[5pt]
-
& =\int\limits_{-4}^{4}{\left( 6-\frac{3}{8}x^{2} \right)}\,dx \\
+
&= \Bigl[\ 6x-\frac{3}{8}\frac{x^3}{3}\ \Bigr]_{-4}^{4}\\[5pt]
-
& =\left[ 6x-\frac{3}{8}\frac{x^{3}}{3} \right]_{-4}^{4} \\
+
&= \Bigl[\ 6x-\frac{x^3}{8}\ \Bigr]_{-4}^{4}\\[5pt]
-
& =\left[ 6x-\frac{x^{3}}{8} \right]_{-4}^{4} \\
+
&= 6\cdot 4 - \frac{4^3}{8} - \Bigl(6\cdot (-4) - \frac{(-4)^3}{8}\Bigr)\\[5pt]
-
& =6\centerdot 4-\frac{4^{3}}{8}-\left( 6\left( -4 \right)-\frac{\left( -4 \right)^{3}}{8} \right) \\
+
&= 24-8+24-8\\[5pt]
-
& =24-8+24-8=32 \\
+
&= 32\,\textrm{.}
-
\end{align}</math>
+
\end{align}</math>}}

Version vom 14:25, 21. Okt. 2008

First, we need a picture of what the region looks like.

Both curves, y=x24+2 and y=8−x28, are parabolas, the first with a minimum value y=2 when x=0, and the second with a maximum value of y=8 when x=0. Roughly speaking, the curves have the appearance shown in the figure below, where the shaded region whose area we are trying to find lies between the curves.

The region is bounded above by the parabola y=8−x28 and below by the parabola y=x24+2. If we can determine the x-coordinates, x=a and x=b, for the points of intersection between the curves, the area we are looking for will be given by

Area=ba8−81x2−41x2+2dx. 

The integrand is the y-value for the upper parabola minus the corresponding y-value for the lower parabola.

At the points where the curves intersect each other, the x- and y-coordinates are equal, which gives the equation system,

yy=8−81x2=41x2+2.

If we eliminate y from this system, we get the following equation for x,

8−81x2=41x2+2.

If we move the x2-terms onto one side and the constants onto the other, we obtain

41x2+81x2=8−2

i.e.

41+81x283x2x2=6=6=16.

The x-coordinates of the points of intersection are therefore equal to x=−4 and x=4.

The area of the area between the curves is given by

Area=4−48−81x2−41x2+2dx=4−48−81x2−41x2−2dx=4−46−81+41x2dx=4−46−83x2dx= 6x−833x3 4−4= 6x−8x3 4−4=64−843−6(−4)−8(−4)3=24−8+24−8=32.
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:4c“