Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 1.3:4

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 5: Zeile 5:
The area of the rectangle is then given by
The area of the rectangle is then given by
-
{{Displayed math||<math>A(x) = \text{(base)}\cdot\text{(height)} = x\cdot (1-x^2)</math>}}
+
{{Abgesetzte Formel||<math>A(x) = \text{(base)}\cdot\text{(height)} = x\cdot (1-x^2)</math>}}
and we will try to choose <math>x</math> so that this area function is maximised.
and we will try to choose <math>x</math> so that this area function is maximised.
Zeile 21: Zeile 21:
We must therefore conclude that the maximum area is a critical point. We differentiate
We must therefore conclude that the maximum area is a critical point. We differentiate
-
{{Displayed math||<math>A'(x) = 1\cdot (1-x^2) + x\cdot (-2x) = 1-3x^2\,,</math>}}
+
{{Abgesetzte Formel||<math>A'(x) = 1\cdot (1-x^2) + x\cdot (-2x) = 1-3x^2\,,</math>}}
and the condition that the derivative should be zero gives that <math>x=\pm 1/\!\sqrt{3}</math>; however, it is only <math>x=1/\!\sqrt{3}</math> which satisfies <math>0\le x\le 1</math>.
and the condition that the derivative should be zero gives that <math>x=\pm 1/\!\sqrt{3}</math>; however, it is only <math>x=1/\!\sqrt{3}</math> which satisfies <math>0\le x\le 1</math>.
Zeile 27: Zeile 27:
At the critical point, the second derivative <math>A''(x)=-6x</math> has the value
At the critical point, the second derivative <math>A''(x)=-6x</math> has the value
-
{{Displayed math||<math>A''\bigl( 1/\!\sqrt{3}\bigr) = -6\cdot\frac{1}{\sqrt{3}} < 0\,,</math>}}
+
{{Abgesetzte Formel||<math>A''\bigl( 1/\!\sqrt{3}\bigr) = -6\cdot\frac{1}{\sqrt{3}} < 0\,,</math>}}
which shows that <math>x=1/\!\sqrt{3}</math> is a local maximum.
which shows that <math>x=1/\!\sqrt{3}</math> is a local maximum.
Zeile 33: Zeile 33:
The answer is that the point <math>P</math> should be chosen so that
The answer is that the point <math>P</math> should be chosen so that
-
{{Displayed math||<math>P = \Bigl(\frac{1}{\sqrt{3}}, 1-\Bigl(\frac{1}{\sqrt{3}} \Bigr)^2\, \Bigr) = \Bigl(\frac{1}{\sqrt{3}}, \frac{2}{3} \Bigr)\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>P = \Bigl(\frac{1}{\sqrt{3}}, 1-\Bigl(\frac{1}{\sqrt{3}} \Bigr)^2\, \Bigr) = \Bigl(\frac{1}{\sqrt{3}}, \frac{2}{3} \Bigr)\,\textrm{.}</math>}}

Version vom 12:56, 10. Mär. 2009

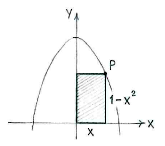
If we call the x-coordinate of the point P x, then its y-coordinate is 1−x2, because P lies on the curve y=1−x2.

The area of the rectangle is then given by

A(x)=(base)(height)=x(1−x2)

and we will try to choose x so that this area function is maximised.

To begin with, we note that, because P should lie in the first quadrant, x0 and also y=1−x20, i.e. x1. We should therefore look for the maximum of A(x) when 0x1.

There are three types of points which can maximise the area function:

  1. critical points,
  2. points where the function is not differentiable,
  3. endpoints of the region of definition.

The function A(x)=x(1−x2) is differentiable everywhere, so item 2 does not apply. In addition, A(0)=A(1)=0, so the endpoints in item 3 cannot be maximum points (but rather the opposite, i.e. minimum points).

We must therefore conclude that the maximum area is a critical point. We differentiate

A(x)=1(1−x2)+x(−2x)=1−3x2

and the condition that the derivative should be zero gives that x=13 ; however, it is only x=13  which satisfies 0x1.

At the critical point, the second derivative A(x)=−6x has the value

A13=−6130 

which shows that x=13  is a local maximum.

The answer is that the point P should be chosen so that

P=131−132=1332. 
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:4“