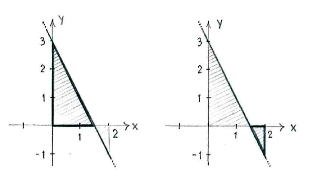Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 2.1:1c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
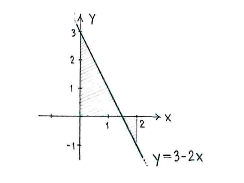
The straight line <math>y=3-2x</math> cuts the ''x''-axis at the point
The straight line <math>y=3-2x</math> cuts the ''x''-axis at the point
-
{{Displayed math||<math>y=3-2x=0\quad \Leftrightarrow \quad x=3/2</math>}}
+
{{Abgesetzte Formel||<math>y=3-2x=0\quad \Leftrightarrow \quad x=3/2</math>}}
so the part of the line to the right of <math>x=3/2</math> lies under the ''y''-axis.
so the part of the line to the right of <math>x=3/2</math> lies under the ''y''-axis.
Zeile 15: Zeile 15:
We obtain
We obtain
-
{{Displayed math||<math>\int\limits_{0}^{2} (3-2x)\,dx = \frac{1}{2}\cdot\frac{3}{2}\cdot 3 - \frac{1}{2}\cdot\frac{1}{2}\cdot 1 = \frac{9}{4} - \frac{1}{4} = 2\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>\int\limits_{0}^{2} (3-2x)\,dx = \frac{1}{2}\cdot\frac{3}{2}\cdot 3 - \frac{1}{2}\cdot\frac{1}{2}\cdot 1 = \frac{9}{4} - \frac{1}{4} = 2\,\textrm{.}</math>}}

Version vom 12:57, 10. Mär. 2009

The straight line y=3−2x cuts the x-axis at the point

y=3−2x=0x=32

so the part of the line to the right of x=32 lies under the y-axis.

When the curve of a function lies both above and below the x-axis, the value of the integral can be interpreted as “an area having a sign”, which means that, for that part where the curve is under the x-axis, we instead subtract the area between the curve and the x-axis.

If we divide up the area between the straight line and the x-axis at x=32, we see that the value of the integral is the area of the triangle to the left in the figure below, minus the area of the triangle to the right.

We obtain

20(3−2x)dx=21233−21211=49−41=2. 
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:1c“