Lösung 2.1:1b

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
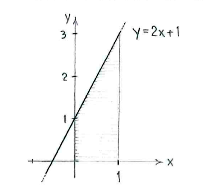
The graph of the function
+
The graph of the function <math>y=2x+1</math> is a straight line which cuts the ''y''-axis at <math>y=1</math> and has slope 2.
-
<math>y=2x+1</math>
+
-
is a straight line which cuts the
+
-
<math>y</math>
+
-
-axis at
+
-
<math>y=\text{1}</math>
+
-
and has gradient
+
-
<math>2</math>.
+
-
 
+
-
The integral's value is the area under the straight line and between
+
-
<math>x=0\text{ }</math>
+
-
and
+
-
<math>x=\text{1}</math>.
+
-
 
+
 +
The integral's value is the area under the straight line and between <math>x=0</math>
 +
and <math>x=1</math>.
[[Image:2_1_1_b1.gif|center]]
[[Image:2_1_1_b1.gif|center]]
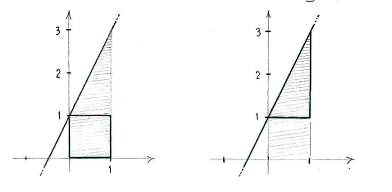
We can divide up the region under the graph into a square and rectangle,
We can divide up the region under the graph into a square and rectangle,
- 
[[Image:2_1_1_b2.gif|center]]
[[Image:2_1_1_b2.gif|center]]
Zeile 26: Zeile 14:
The value of the integral is
The value of the integral is
-
 
+
{{Displayed math||<math>\begin{align}
-
<math>\int\limits_{0}^{1}{\left( 2x+1 \right)\,}dx=</math>
+
\int\limits_{0}^{1} (2x+1)\,dx
-
(area of the square) + (area of the triangle)
+
&= \text{(area of the square)} + \text{(area of the triangle)}\\
-
<math>1\centerdot 1+\frac{1}{2}\centerdot 1\centerdot 2=2</math>
+
&= 1\cdot 1 + \frac{1}{2}\cdot 1\cdot 2 = 2\,\textrm{.}
 +
\end{align}</math>}}

Version vom 12:09, 21. Okt. 2008

The graph of the function \displaystyle y=2x+1 is a straight line which cuts the y-axis at \displaystyle y=1 and has slope 2.

The integral's value is the area under the straight line and between \displaystyle x=0 and \displaystyle x=1.

We can divide up the region under the graph into a square and rectangle,

and then add up the area to obtain the total area.

The value of the integral is

\displaystyle \begin{align}

\int\limits_{0}^{1} (2x+1)\,dx &= \text{(area of the square)} + \text{(area of the triangle)}\\ &= 1\cdot 1 + \frac{1}{2}\cdot 1\cdot 2 = 2\,\textrm{.} \end{align}

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:1b“