Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 3.2:2e

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
 
Because the expression contains both <math>z</math> and <math>\bar{z}</math>, we write out <math>z=x+iy</math>, where <math>x</math> is the real part of <math>z</math> and <math>y</math> is the imaginary part. Thus, we have
Because the expression contains both <math>z</math> and <math>\bar{z}</math>, we write out <math>z=x+iy</math>, where <math>x</math> is the real part of <math>z</math> and <math>y</math> is the imaginary part. Thus, we have
-
<math>\mathrm{Re}z=x</math>
+
:*<math>\mathop{\rm Re}z = x</math>
-
 
+
:*<math>i+\bar{z} = i+(x-iy) = x+(1-y)i</math>
-
<math>i+\bar{z}=i+(x-iy)=x+(1-y)i</math>
+
and the condition becomes
and the condition becomes
-
<math>x=x+(1-y)i \iff 0=(1-y)i</math>
+
{{Displayed math||<math>x=x+(1-y)i\quad\Leftrightarrow\quad 0=(1-y)i</math>}}
which means that <math>y=1</math>.
which means that <math>y=1</math>.
-
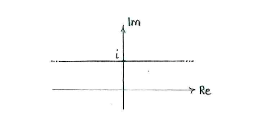
The set therefore consists of all complex numbers with imaginary part <math>1</math>.
+
The set therefore consists of all complex numbers with imaginary part 1.
[[Image:3_2_2_e.gif|center]]
[[Image:3_2_2_e.gif|center]]
- 
-
{{NAVCONTENT_STOP}}
 

Version vom 09:44, 29. Okt. 2008

Because the expression contains both z and z, we write out z=x+iy, where x is the real part of z and y is the imaginary part. Thus, we have

  • Rez=x
  • i+z=i+(x−iy)=x+(1−y)i

and the condition becomes

x=x+(1−y)i0=(1−y)i

which means that y=1.

The set therefore consists of all complex numbers with imaginary part 1.

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:2e“