Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Binomialkoeffizient

Aus Online Mathematik Brückenkurs 1

Wechseln zu: Navigation, Suche

Eigenschaften des Binomialkoeffizienten

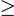kn=n!(n−k)!k!  mit nNkNnk

Beispiel 1

  1. kn=nn−k 
    nn−k=n!(n−n+k)!(n−k)!=n!(k)!(n−k)!=kn 
  2. 0n=1 
    0n=n!(n−0)!0!=n!n!1=n!n!=1 
  3. 1n=n 
    1n=n!(n−1)!1!=n!n(n−1)!n=n!n!n=n 
  4. nn=1 
    nn=n!(n−n)!n!=n!0!n!=n!1n!=1 
  5. nn−1=n 
    nn−1=n!(n−n+1)!(n−1)!=n!1!(n−1)!=n!n(n−1)!n=n!n!n=n 
  6. kn−1+k−1n−1=kn 
    kn−1+k−1n−1=(n−1)!(n−1−k)!k!+(n−1)!(n−1−(k−1))!(k−1)! 
    =(n−1)!(n−1−k)!k!+(n−1)!k(n−k)!(k−1)!k=(n−1)!(n−k)(n−1−k)!k!(n−k)+(n−1)!k(n−k)!k!
    =(n−k)!k!(n−1)!(n−k)+(n−1)!k(n−k)!k!=(n−k)!k!(n−1)!(n−k)+(n−1)!k=(n−k)!k!(n−1)!(n−k+k)
    =(n−1)!n(n−k)!k!=n!(n−k)!k!=kn 

Das Paskalsche Dreieck

00 
01   11 
02   12   22 
03   13   23   33 
04   14   24   34   44 
1
1    1
1    2    1
1    3    3    1
1    4    6    4    1
Das Paskalsche Dreieck
Von „http://wiki.math.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/Binomialkoeffizient“