1.1 Observatörer i vila
Relativitetsteori
Innehåll:
Detta avsnitt handlar om olika observatörer i vila i förhållande till varandra.
Lärandemål:
Efter detta avsnitt ska du kunna:
- utföra translationer och enkla rotationer på koordinater,
- definiera hur längd mäts i koordinatsystem som är i vila,
- redogöra för vad begreppet invariant betyder i fysiken.
Olika observatörer i vila relativt varandra
Relativitet har att göra med hur olika observatörer uppfattar ett fysikaliskt förlopp. När vi mäter ett fysikaliskt fenomen, t.ex. längden av en stav i laboratoriet, så vet vi av erfarenhet att längden inte ändras om jag vrider staven ett halvt varv eller flyttar den i sidled ett stycke. Denna egenskap, att längden hos ett föremål inte beror av vilket läge den intar i rummet brukar uttryckas som att längden är invariant under förflyttningar, som kallas translationer med ett fint ord, samt rotationer. När vi uttrycker detta i matematisk form inför vi av praktiska skäl ett koordinatsystem, med \displaystyle x-, \displaystyle y- och \displaystyle z-axlar i rummet. Detta koordinatsystem kallar vi \displaystyle S och är det som observatören \displaystyle O, som befinner sig i origo i \displaystyle S använder.
Definition: Med längd menar vi en sträcka som mäts upp med en standardmåttstock som befinner sig i vila i observatörens system.
Längden \displaystyle L hos staven kan då skrivas
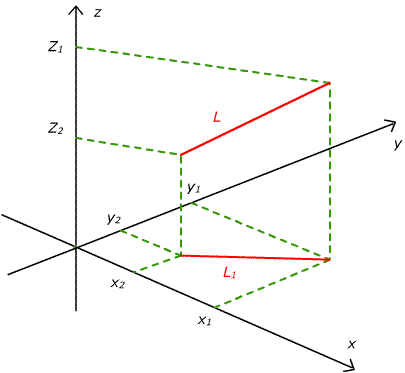
(enligt Pytagoras sats, se nedanstående figur) som
\displaystyle L = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 +(z_1-z_2)^2}, (1.1)
där \displaystyle (x_1, y_1,z_1) och \displaystyle (x_2,y_2, z_2) är stavens bägge respektive ändpunkter. Om staven flyttas ett stycke betyder det att koordinaterna \displaystyle x_1 och \displaystyle x_2 ändras med samma värde, och motsvarande för de två andra koordinaterna. Detta är ekvivalent med att vi i stället flyttar origo i kooridinatsystemt i motsatt riktning till ett nytt läge. Det nya koordinatsystemet kallar vi \displaystyle S', och observatören i det för \displaystyle O', även om det i detta enkla fall kan vara samma person. Det är uppenbart att eftersom längden \displaystyle L bara beror av skillnaderna hos ändpunkternas koordinater, \displaystyle L då kommer att vara oförändrad, eller invariant, om vi i stället låter den uttryckas i \displaystyle O's koordinatsystem \displaystyle S'.
Längden \displaystyle L av en stav kan beräknas genom att tillämpa Pythagoras sats två gånger. Låt \displaystyle L_1 vara projektionen av \displaystyle L i \displaystyle x−y planet. Vi kan då bilda en rätvinklig trangel där hypotenusan utgörs av \displaystyle L_1 och kateterna av \displaystyle (x_1−x_2) och \displaystyle (y_1−y_2). Pythagoras sats ger då att \displaystyle L^2_1=(x_1−x_2)^2+(y_1−y_2)^2. Vi ser vidare att vi kan bilda ytterilgare en rätvinklig triangel med \displaystyle L som hypotenusa och \displaystyle L_1 samt \displaystyle (z_1−z_2) som kateter. Ytterligare en tillämning av Pythagoras sats ger då \displaystyle L_2=L^2_1+(z_1−z)^2=(x_1−x_2)^2+(y_1−y_2)^2+(z_1−z_2)^2.
Exempel 1
En boll befinner sig i punkten (x,y,x)=(1,1,0). Om bollen rullar en meter i x led och en meter i y-led blir dess nya koordinater (x',y',z')=(2,2,0). Samma resultat uppnår vi om vi flyttar origo för vårt koordinatsystem en meter bakåt i x och y led. Matematiskt kan vi uttrycka relationen mellan de nya koordinaterna (x',y',z') och de gamla koordinaterna (x,y,z) som
\displaystyle x' = x +1, (1.2)
\displaystyle y' = y+1, (1.3)
\displaystyle z' = z. (1.4)
Exempel 2
Antag att en stav har ändpunkterna (0,0,0) och (1,2,3) i koordinatsystemet S. Vi kan då beräkna dess längd till \displaystyle L = \sqrt{(0-1)^2 + (0-2)^2 +(0-3)^2}= \sqrt{14}. Om staven nu förskjuts en sträcka \displaystyle \Delta x = 2 i x-led och \displaystyle \Delta y = 2 i y-led och \displaystyle \Delta z = 3 i z-led blir relationen mellan nya och gamla koordinater
\displaystyle x' = x +\Delta x = x+2 (1.5)
\displaystyle y' = y +\Delta y = y+2 (1.6)
- \displaystyle z' = z +\Delta z = z+3
och dess nya ändpunkter (2,2,3) och (3,4,6). Vi kan dock kontrollera att dess längd är invariant: \displaystyle L = \sqrt{(2-3)^2 + (2-4)^2 +(3-6)^2}= \sqrt{14}.
Rotationer
På samma sätt vet vi att en rotation av koordinatsystemet inte heller ändrar stavens längd. En rotation har egenskapen att om koordinataxlarna \displaystyle x,y,z i det ursprungliga koordinatsystemet \displaystyle S är ortogonala så kommer även de roterade koordinataxlarna \displaystyle x',y',z' i \displaystyle S' att vara ortogonala.
Räkningarna i rutan nedan visar
nu att \displaystyle L(x',y',z') = L(x,y,z) = L, där
man använder kända samband för de trigonometriska
funktionerna, speciellt att
| \displaystyle \sin^2 \theta + \cos^2 \theta = 1, |
vars geometriska tolkning är just Pythagoras sats. Projektionen av staven i \displaystyle xy-planet är ju hypotenusan i en rätvinklig triangel om koordinataxlarna är ortogonala, och denna hypotenusa är alltså oförändrad till sin längd i de nya koordinaterna, vilket är just kravet att de nya primmade koordinataxlarna är ortogonala.
Detaljer för den intresserade:
Rotationer som ges av ortogonala transformationer kan skrivas som ett system av linjära ekvationer som följer.
Om vi roterar en vinkel \displaystyle \theta kring \displaystyle z-axeln, blir de nya koordinaterna:
x' = x \cos \theta - y \sin\theta,
y' = x \sin \theta + y \cos\theta,
z' = z.
Eftersom vi vrider runt \displaystyle z-axeln förändras inte \displaystyle z-koordinaten. Om vi nu uttrycker \displaystyle L i det primmade systemet \displaystyle S':s koordinater i stället, kan vi, med hjälp av transformationen ovan, lätt räkna ut att \displaystyle L fortfarande har samma värde som förut. Det enklaste är att först lägga stavens ena ändpunkt i origo, eftersom vi kan göra godtyckliga förflyttningar av staven utan att dess längd ändras enligt vad vi nyss lärde. Med andra ord låter vi origo för \displaystyle S och \displaystyle S' sammanfalla, så att \displaystyle x_2=y_2=z_2=0 och \displaystyle x_1=x, \displaystyle y_1=y och \displaystyle z_1=z. Längden av staven kan då skrivas
L = L(x,y,z) = \sqrt{x^2+y^2+z^2},
där den ändpunkt som inte ligger i origo nu helt enkelt har koordinaterna \displaystyle x,y,z. Det är nu lätt att sätta in de roterade koordinaterna i stället: \displaystyle L= L(x',y',z').
Exempel 3 (för den intresserade)
Visa sambandet \displaystyle L(x',y',z') = L(x,y,z) = L för rotationer genom att sätta in koordinaternas uttryck från ekvationerna ovan.
 Hämtar...
Hämtar...