Relativitetsteori

Tiden som en fjärde dimension

Vi har sett att tiden multiplicerad med ljushastigheten \displaystyle c har samma dimension som längdkoordinaterna, och därför kan uppfattas som en fjärde dimension. Detta är numera standard inom den moderna matematiska framställningen av den speciella relativitetsteorin och ligger till grund för den allmänna relativitetsteorin. Den har sin rötter i en gammal dröm om att geometrisera rörelse. Denna strävan går tillbaks till grekerna, som menade att rörelsen var en synvilla. Främst Archimedes strävade efter att finna en geometrisk beskrivning av rörelse. Den geometrisering som vi talar om här är inte den som diskuterades senare av Kepler och Galilei, som diskuterade rörelse i termer av banor med geometrisk form: ellipser, parabler och hyperbler. Dessa s.k. kägelsnitt (eller koniska sektioner) är visserligen geometriska, men partiklarna rör sig fortfarande längs dessa kurvor i rummet.

Idén om en fjärde dimension dök upp igen under 1800-talet. Det var speciellt tysken Gustav Fechner, som skrev om den fjärde dimensionen om än med en något annan vinkling än vad vi syftar till. Senare introducerade den engelske science-fictionförfattaren H. G. Wells tiden som en fjärde dimension i sin roman Tidsmaskinen, från 1895. Fortfarande i Einsteins arbete från 1905, finns inte tiden med som en fjärde dimension.

Det var Einsteins tidigare lärare från ETH i Zürich, Hermann Minkowski, som snart efter Einsteins publicering av den speciella relativitetsteorin insåg att denna med fördel kunde formuleras matematiskt mycket elegant om man inför ett fyrdimensionellt rum-tidskontinuum, Minkowskirummet, \displaystyle M. Han publicerade resultatet år 1908, strax innan han alltför tidigt hastigt gick bort. För att följa Minkowski i spåren måste vi multiplicera tiden med den universella ljushastigheten \displaystyle c, som är densamma för alla observatörer som är relaterade till varandra via Lorentztransformationer. Rörelsen hos en partikel med konstant hastighet kan då representeras med en rät linje i \displaystyle M, och alla teorem om räta linjer i \displaystyle M utsäger något om rörelse av fria partiklar med konstant hastighet. I samma anda kommer krökta linjer beskriva partiklar som påverkas av krafter, dvs retarderande eller accelererande partiklar. På detta sätt kan rörelse beskrivas geometrisk, och Archimedes gamla dröm har på ett sätt gått i uppfyllelse.

Intervallet \displaystyle s^2 spelar i Minkowskirummet en roll som är analog med längden \displaystyle L för det Euklidiska rummet. Eftersom \displaystyle s^2 inte alltid är positivt är det dock inte fysikaliskt meningsfullt att dra roten ur det.

I det fyrdimensionella Minkowskirummet beskrivs partiklarna inte av banor utan av världslinjer. Dessa världslinjer representerar partikelns rumtidshistoria. Om en partikel rör sig i t.ex. en Keplerbana, kommer dess världslinje att vara spiralformad (dvs en hyperspiral) i \displaystyle M.

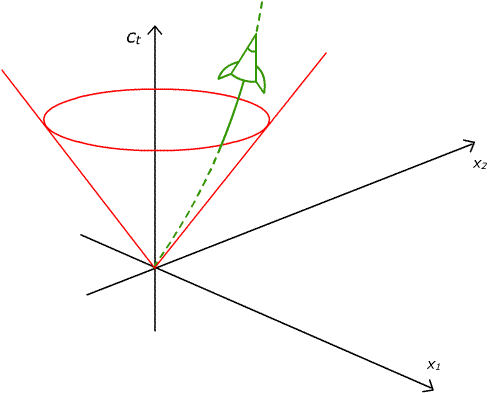
För ljuset kommer dess världslinje alltid att ligga på den kurva som beskrivs av \displaystyle s^2=0. I Minkowskirummet kommer detta betyda att ljuset alltid ligger på en hyperkon, den s.k. ljuskonen. En massiv partikel rör sig å andra sidan alltid med en hastighet som är mindre än \displaystyle c och dess världslinje ligger därför alltid innanför ljuskonen, med ett tidslikt intervall. Detta illustreras i figuren nedan där ett (massivt) rymdskepp rör sig innanför ljuskonen.

Ett fixt tidslikt intervall blir en hyperhyperboloid i Minkowskirummet osv. Den här geometriska beskrivningen blir nu nära förknippad med det som vi tidigare kallade symmetri. Alla symmetritransformationer av räta linjer eller spiraler, hyperkoner, hyperhyperboloider osv kommer ha någonting att säga om all möjliga symmetritransformationer av partiklars rörelse. Och geometriska symmetrier är ganska väl studerade.