3.5 Relativistiska reaktioner
Relativitetsteori
Lärandemål:
Efter detta avsnitt ska du kunna:
- Veta vad som är laboratoriesystemet respektive tyngdpunktssystemet.
- Kunna beräkna energi- och rörelsemängdsförändringar i reaktioner mellan relativistiska elementarpartiklar med hjälp av Lorentzinvarianter.
En viktig tillämpning av den speciella
relativitetsteorin ligger i att beräkna energi- och
rörelsemängdsförändringar vid reaktionsförlopp mellan
elementarpartiklar. Det beror bl. a. på att partiklarna
rör sig med höga hastigheter, så att deras kinetiska
energier är av samma storleksordning eller rent av
mycket större än energin i deras vilomassor. Med andra
ord är ofta
\displaystyle p/mc\geq 1.
En annan orsak är, som vi såg ovan, att massa och
energi kan transformeras över i varandra. Partiklar kan
därför skapas och förintas vid kollisionsprocesser.
|
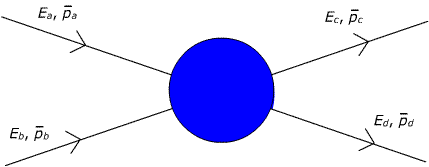
I figuren ovan anges ett typiskt diagram för en kollision mellan två partiklar. De utgående partiklarna kan vara de samma som de ingående. Då talar man om elastiska kollisioner. De kan också vara två andra partiklar, vilket sker vid inelastiska kollisioner. Vi har fyra konserveringslagar som skall vara uppfyllda vid kollisionen: energin, \displaystyle E, skall bevaras för och efter kollisionen, liksom de tre komponenterna av rörelsemängdsmomentet \displaystyle \bar p.
Med beteckningar som i figuren blir de fyra
ekvationerna:
| (3.36) |
| (3.37) |
Nu är både energin och rörelsemängden additiva. Den totala energin och rörelsemängden före kollisionen är \displaystyle E_i= E_a + E_b och \displaystyle \bar p_i = \bar p_a +\bar p_b, medan de motsvarande storheterna efter kollisionen är \displaystyle E_f= E_c + E_d och \displaystyle \bar p_f = \bar p_c +\bar p_d. I samtliga dessa fall gäller givetvis att intervallen \displaystyle s^2(E_k/c, \bar p_k) = (E_k/c)^2-\bar p_k^2 \geq 0, för \displaystyle k= i, f, a, b, c, d är invarianta under Lorentztransformationer.
Dessutom gäller att
| (3.38) |
vilket följer ur ekvationerna för energi och rörelsemängdskonservering, om man kvadrerar höger och vänsterleden.
Detta har stor betydelse, eftersom vi kan räkna ut
uttrycket \displaystyle s^2(E_k/c, \bar p_k) i ett
godtyckligt system, där det av något skäl är
enklast. En av hemligheterna vid beräkningar med
relativitetsteorin är just att använda sig av
invarianta uttryck för att slippa göra explicita
Lorentztransformationer.
Ofta är det två system som är vanligt förekommande,
nämligen laboratoriesystemet och
tyngdpunktssystemet.
a) I laboratoriesystemet är den ena partikeln, säg \displaystyle b, i vila före kollisionen, dvs vi har \displaystyle \bar p_b = 0 och \displaystyle E_b = m_bc^2.
b) I tyngdpunktssystemet gäller att totala
rörelsemängden är noll före och efter kollisionen, dvs
\displaystyle \bar p_a +\bar p_b = \bar p_c +\bar p_d =
0. Det betyder att partiklarna kolliderar med
lika stora men motriktade rörelsemängder:
\displaystyle \bar p_a = -\bar p_b = \bar p.
Efter kollisionen lämnar de nya partiklarna
kollisionsområdet med motriktade rörelsemängder:
\displaystyle \bar p_c = -\bar p_d.
I dessa fall gäller givetvis att
\displaystyle E_a= c \sqrt{m_a^2c^2 + \bar p^2} och
\displaystyle E_b=c \sqrt{m_b^2c^2+\bar p^2}, och
motsvarande för energierna efter kollisionen.
Exempel
Låt oss tillämpa detta på ett exempel med en foton som kolliderar med en proton och bildar en neutron och en positivt laddad pimeson. Reaktionen är alltså
|
Massan är noll för fotonen och lika med \displaystyle m_p, \displaystyle m_n och \displaystyle m_{\pi} för de andra tre partiklarna. Vi frågar nu vid vilken minsta energi hos fotonen i laboratoriesystemet denna reaktion är möjlig.
I laboratoriesystemet är protonen i vila, dvs
\displaystyle \bar p_p=0
och \displaystyle E_a = m_p c^2. Hur skall vi nu
räkna ut tröskelenergin? I vilosystemet för
partiklarna borde den minsta energin krävas när de
nybildade partiklarna just skapats, men befinner sig i
vila. Det betyder att
\displaystyle \bar p_n = \bar p_{\pi} =0, och
\displaystyle E_n = m_n c^2 liksom
\displaystyle E_{\pi}= m_{\pi}c^2. Tyvärr beskriver vi
här situationen för reaktionen i två olika system, och
borde göra en Lorentztransformation mellan dem. Om vi
nu använder de invarianta intervallen i stället,
behöver vi inte bekymra oss om i vilket Lorentzsystem
vi räknar. Tröskelenergin i sluttillståndet är alltså
\displaystyle E_f = m_n c^2 +m_{\pi}c^2 och
\displaystyle \bar p_f =0.
Begynnelseenergin är
\displaystyle E_i = E_{\gamma}+ m_p c^2 medan
rörelsemängden är
\displaystyle \bar p_i = \bar p_{\gamma}. Vi sätter
nu in dessa uttryck i respektive intervall och sätter
dessa lika:
| (3.39) |
Om vi beräknar vänsterledet först får vi:
| (3.40) |
där vi använt att fotonen är masslös, varför \displaystyle E_{\gamma}= \left|\bar p_{\gamma}\right|c.
Det producerade partikelparets intervall är å andra
sidan
\displaystyle s^2((m_n +m_{\pi})c,\bar 0)
=(m_n+m_{\pi})^2c^2.
Om vi sätter de två intervallen lika finner vi
| (3.41) |
Ur detta kan vi lösa ut fotonenergin i laboratoriesystemet som
| (3.42) |
Med insatta värden: \displaystyle m_p \approx m_n \approx 940 MeV; \displaystyle m_{\pi}= 140 MeV finner man att \displaystyle E_{\gamma}\approx 151 MeV, dvs lite mer än viloenergin för pimesonen.
Om vi begrundar vad som händer ovanför tröskeln, ser vi
att vi bara behöver byta ut intervallet för
sluttillståndet mot uttrycket
\displaystyle s^2((E_n+E_{\pi}),\bar 0)=
(E_n+E_{\pi})^2/c^2.
Här är
\displaystyle E_n = m_nc^2 +K_n och
\displaystyle E_{\pi}=m_{\pi}c^2+K_{\pi}.
Det är alltså de kinetiska energierna för neutronen och
pimesonen som drar energi ovanför tröskeln.
Eftersom det finns många olika elementarpartiklar och många olika sluttillstånd för reaktionerna, kan den här typen av problem varieras i nära nog oändligheten. Förutom energi och rörelsemängd finns ett antal andra konserveringslagar, t. ex för elektrisk laddning, samt vissa andra kvanttal, vilka också måste vara uppfyllda.
Det finns också många olika metoder att beräkna
energierna. Man kan t.ex. först beräkna fotonenergin i
tyngdpunktssystemt och sedan göra en
Lorentztransformation till laboratoriesystemet,
alternativt använda Dopplereffekten för att beräkna
frekvensändringen hos fotonen mellan
tyngdpunktssystemet och laboratoriesystemet.
Exempel
I Celsius-acceleratorn i The Svedberglaboratoriet i Uppsala vill man studera reaktionen
|
genom att skjuta protoner på en fast deuteriumtarget. Här är \displaystyle p protoner, \displaystyle n en neutron, \displaystyle d en deutron och \displaystyle \eta en oladdad meson kalla <q>äta</q>. Ätamesonens massa vet man är 550 MeV. Protonens massa är ca \displaystyle 940 MeV. Den tillgängliga kinetiska energin \displaystyle T_p för protonerna i acceleratorn var vid den här tiden \displaystyle T_p = 700 MeV. Skulle reaktionen vara möjlig?
Lösning Före reaktionen är deutronen i vila i laboratoriesystemet, och vi har följade uttryck för det invarianta intervallet
|
|
|
där vi använt \displaystyle m_d\approx 2m_p och \displaystyle E_p =m_pc^2+T_p. För sluttillståndet har vi i dess vilosystem ingen total rörelsemängd, men \displaystyle s^2((m_p+m_p+m_n+m_{\eta})^2/c^2)\approx (3m_p+m_{\eta})^2c^2 . Ur dessa två uttryck, som skall vara lika, kan vi lösa ut \displaystyle T_p, som blir: \displaystyle T_p = m_{\eta}c^2(3/2+ m_{\eta}/4m_p)\geq \frac{13}{8} m_{\eta} \approx 900 MeV, vilket inte räcker.
Övningsuppgift
En väteatom (H) har bindningsenergin \displaystyle B=13.6 eV. Vilken minsta energi måste en foton ha för att reaktionen
|
skall kunna ske, där \displaystyle p är en proton och \displaystyle e är en elektron, eller med andra ord vilken fotonenergi krävs för att att en foton kan slå ut en elektron från en väteatom i vila. Denna reaktion liknar fotoeffekten: fotonen måste övervinna elektronens bindningsenergin i väteatomen för att elektronen skall kunna komma ut.
Frågan är: hur mycket extra energi behöver fotonen för att reaktionen skall kunna ske?
Övningsuppgift
I en partikelaccelerator skjuter man en antiproton \displaystyle p^- mot en stillastående proton \displaystyle p^+. Antiprotonen accelereras upp till en hastighet 0.9999 c (i laboratoriesystemet).
Kommer energin att vara tillräcklig för att reaktionen
|
ska kunna inträffa?
Partikeln \displaystyle Z_0 har massan 95.6 GeV/\displaystyle c^2.
 Hämtar...
Hämtar...